超椭圆曲线(八)约化因数相加
令$C$是定义在有限域$K$上属性为$g$的一个超椭圆曲线,令$J$是$C$的雅克比行列式,令$P(x,y)\in C$,令$\sigma$是$\bar K$到$K$的一个自同构,则$P^{\sigma}=(x^{\sigma},y^{\sigma})$同样是$C$上的一个点。
定义48(因数的定义域)若一个因数$D=\sum m_{P}P$有$D^{\sigma}=\sum m_{P}P^{\sigma}$能对任意$\bar K$到$K$的自同构$\sigma$均与$D$相等。
注意到如果$D$定义在$K$上,这并不代表$D$的支撑集中的每个点均为$K$有理点,一个主因数定义在$K$上当且仅当它是一个有$K$中系数的有理函数的因数,$J$中所有除数类的集合$J(K)$有一个定义在$K$上的代表,是$J$的一个子群。$J(K)$的每个元素都有一个唯一的表示形式,即约化因数$div(a, b)$,其中$a,b\in K[u],deg(a)\leq g,deg(b)<deg(a)$,因此$J(K)$事实上是一个有限Abel群。本节介绍一种在该组中元素相加的有效算法。
令$D_{1}=\textrm{div}(a_{1},b_{1}),D_{2}=\textrm{div}(a_{2},b_{2})$为两个在$K$上定义的约化因数(则$a_{1},b_{1},a_{2},b_{2}\in K[u]$)。算法1寻找一个半约化因数$D=\textrm{div}(a,b),a,b\in K[u]$使得$D\sim D_{1}+D_{2}$。算法2将$D$约化为等价的约化因数$D^{‘}$。
算法1,2由Koblitz [20]实现,其推广了Cantor[5]的早期算法—假定$h(u)=0$且$char(K)\neq 2$。

定理49(算法1的有效性)令$D_{1}=\textrm{div}(a_{1},b_{1}),D_{2}=\textrm{div}(a_{2},b_{2})$为两个半约化因数,令$a,b$如式$(4),(5)$定义,则$D=\textrm{div}(a,b)$是一个半约化因数且$D\sim D_{1}+D_{2}$。
证明:
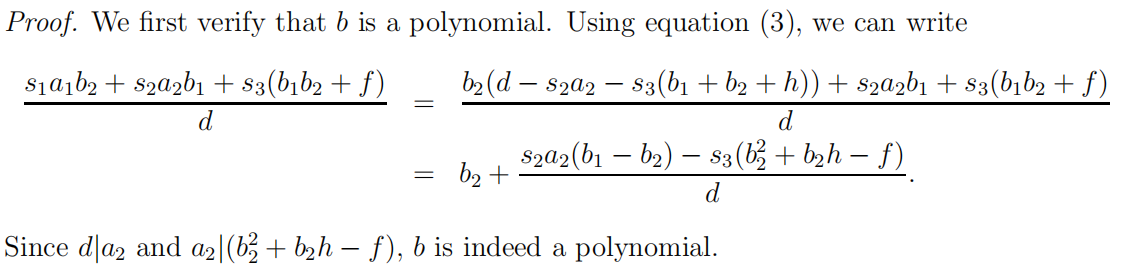



算法2:
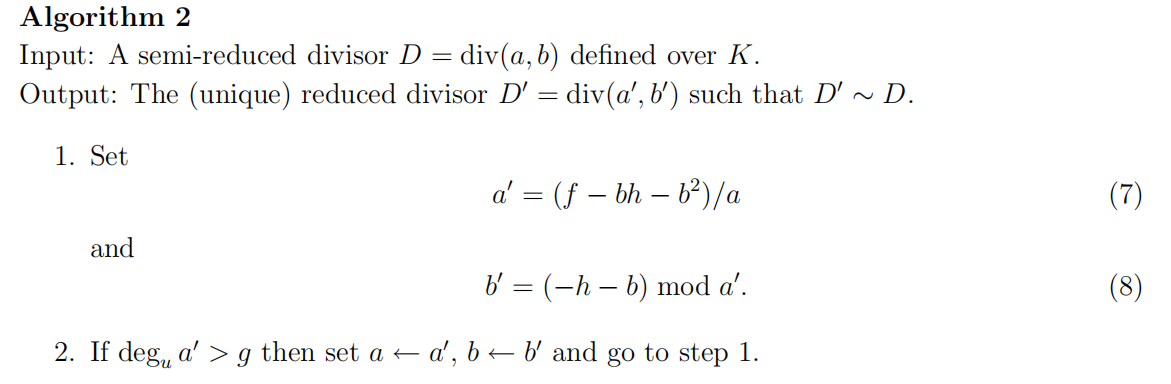

定理51(算法2的有效性)令$D=\textrm{div}(a,b)$是一个半约化因数,则由算法2返回的因数$D^{‘}=\textrm{div}(a^{‘},b^{‘})$是约化的且$D^{‘}\sim D$。
证明:


注意,算法1和算法2中的所有计算都发生在域$K$本身(而不是$K$的任何适当扩展)。在算法1中,若$deg(a_{1})\leq g,deg(a_{2})\leq g$则$deg(a)\leq 2g$。此时,算法2对步骤1的迭代次数最多为$[g/2]$。
