文章目录

本节描述雅可比矩阵半约化因子的多项式表示。它引出了一个有效的算法来添加雅可比矩阵的元素。

引理40 令$P(x,y)$是$C$上一个平凡点，再令$R\in \bar K(C)$是一个在$P$处没有极点的有理函数，则对任意的$k\geq 0$，存在唯一的元素$c_{0},\cdots,c_{k}\in\bar K$与$R_{k}\in \bar K(C)$使得$R=\sum_{i=0}^{k} c_{i}(u-x)^{i}+(u-x)^{k+1}R_{k}$，其中$R_{k}$在$P$处没有极点。

证明：

 

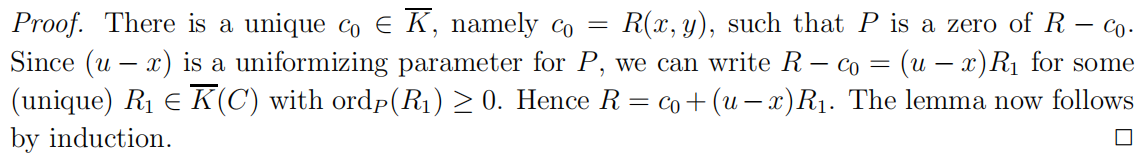
引理41 令$P(x,y)$是$C$上一个平凡点，则对任一$k\geq 1$，存在唯一的多项式$b_{k}(u)\in \bar K[u]$使得：

$\textrm{(i)}\ deg_{u} b_{k}<k$；

$\textrm{(ii)}\ b_{k}(x)=y$且$b_{k}^{2}(u)+b_{k}(u)h(u)\equiv f(u)\ \textrm{mod}\ (u-x)^{k}$；

证明：

 

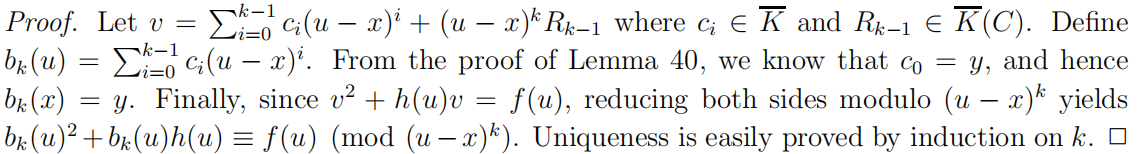
下面的定理说明了半约化因数如何可以表示为两个多项式函数的因数的最大公约数。

定理42 令$D=\sum m_{i}P_{i}-(\sum m_{i})\infty$是一个半约化因数，其中$P_{i}(x_{i},y_{i})$，令$a(u)=\prod (u-x_{i})^{m_{i}}$。令$b(u)$是唯一满足如下条件的多项式：
$\textrm{(i)}\ deg(b)<deg(a)$；

$\textrm{(ii)}$对所有$m_{i}\neq 0$的$i$都有$b(x_{i})=y_{i}$；

$\textrm{(iii)}\ a(u)|[b^{2}(u)+b(u)h(u)-f(u)]$，则$D=\textrm{gcd}(div(a(u)),div(b(u)-v))$。

注：$\textrm{gcd}(div(a(u)),div(b(u)-v))$通常缩写为$div(a(u),b(u)-v)$或者，更简单：$div(a,b)$。

 

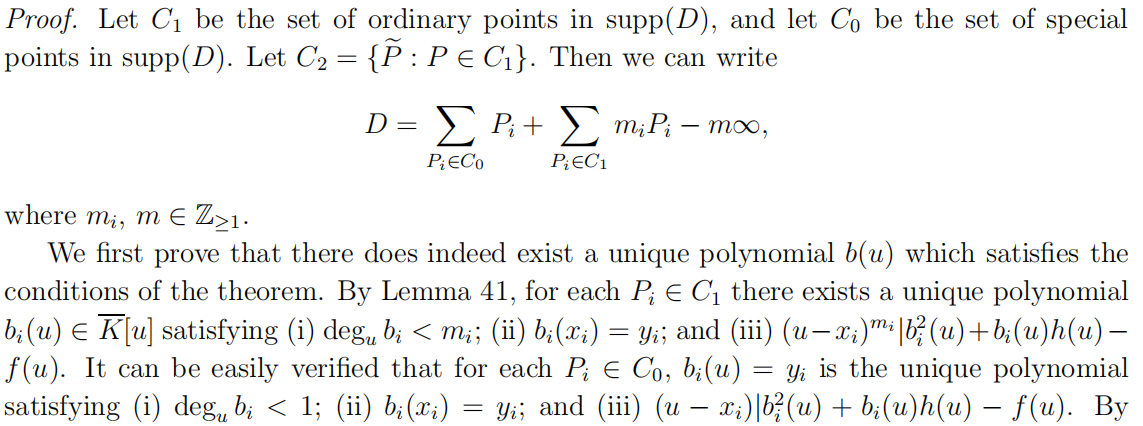
注意到零因数表示为$div(1,0)$，下一个结果来自定理42的证明。

引理43 令$a(u),b(u)\in \bar K[u]$使得$deg(b)<deg(a)$，若$a|(b^{2}+bh-f)$则$div(a,b)$是半约化的。