超椭圆曲线(四)零点与极点
本节介绍单值化参数的概念,以及有理函数的零点和极点的阶数。
定义18(零点,极点)令$R\in \bar K(C)^{*},P\in C$。若$R(P)=0$则记为$R$在$P$有一个零点。若$R$在$P$处没有定义则记为$R$在$P$处有一个极点,此时我们记为$R(P)=\infty$。
引理19令$G\in \bar K(C)^{*},P\in C$,若$G(P)=0$,则$\bar G(\bar P)=0$。
证明:套定义算就行,过程略。
定理23中使用引理20、21和22,证明了单值化参数的存在性。
引理20 令$P(x,y)$是$C$上一个点。假定$G(u,v)=a(u)-b(u)v\in \bar K[C]^{*}$在$P$处有一个零点,且$x$不是$a(u),b(u)$的根。则$\bar G(P)=0$当且仅当$P$是一个特殊点。
证明:式子一列就看出来了。
引理21 令$P(x,y)$是$C$上一个平凡点,$G=a(u)-b(u)v\in \bar K(C)^{*}$。若$G(P)=0$,且$x$不是$a(u),b(u)$的根。则$G$能被写为$(u-x)^{s}S$的形式,其中$s$是$(u-x)$能够整除$N(G)$的最高次数。$S\in \bar K(C)$在$P$处既无零点也无极点。
证明:$G=N(G)/\bar G$,由引理20,$\bar G(P)\neq 0\Rightarrow N(G)(x)=0$,因此$N(G)$可被表示为$(u-x)^{s}d(u)$的形式。再令$S=d(u)/\bar G$,则$G$能被写为$(u-x)^{s}S$的形式。由$s$的定义可知$S(P)\neq 0$且$S(P)\neq \infty$。
引理22 令$P(x,y)$是一个在$C$上的特殊点。则$(u-x)$可被写为$(v-y)^{2}\cdot S(u,v)$,其中$S(u,v)\in \bar K(C)$在$P$处既无零点也无极点。
证明:记$H(u,v)=(v-y)^{2} , s(u)=H(u,y)$,显然$s(x)=0 , s^{‘}(u)=f^{‘}(u)-h^{‘}(u)y$,由于$C$是超椭圆曲线,无奇异点,而$P(x,y)$是特殊点,因此$2y+h(u)=0$,因此必有$f^{‘}(x)-h^{‘}(x)y\neq 0$,即$s^{‘}(x)\neq 0$;综上,$(u-x)|H(u,v)$且$(u-x)^{2}\nmid H(u,v)$,可得$S(x,y)\neq 0,\infty$。
引理23(单值化参数的存在性)令$P\in C$,则存在一个函数$U\in\bar K(C) , U(P)=0$使下列性质成立:对于每个多项式函数$G\in \bar K[C]^{*}$,存在整数$d$与函数$S\in\bar K(C)$,使得$S(P)\neq 0,\infty$且$G=U^{d}S$;此外,$d$与$U$的选择无关。$U$称为关于$P$的单值化参数。
证明:太麻烦了,自己看吧!



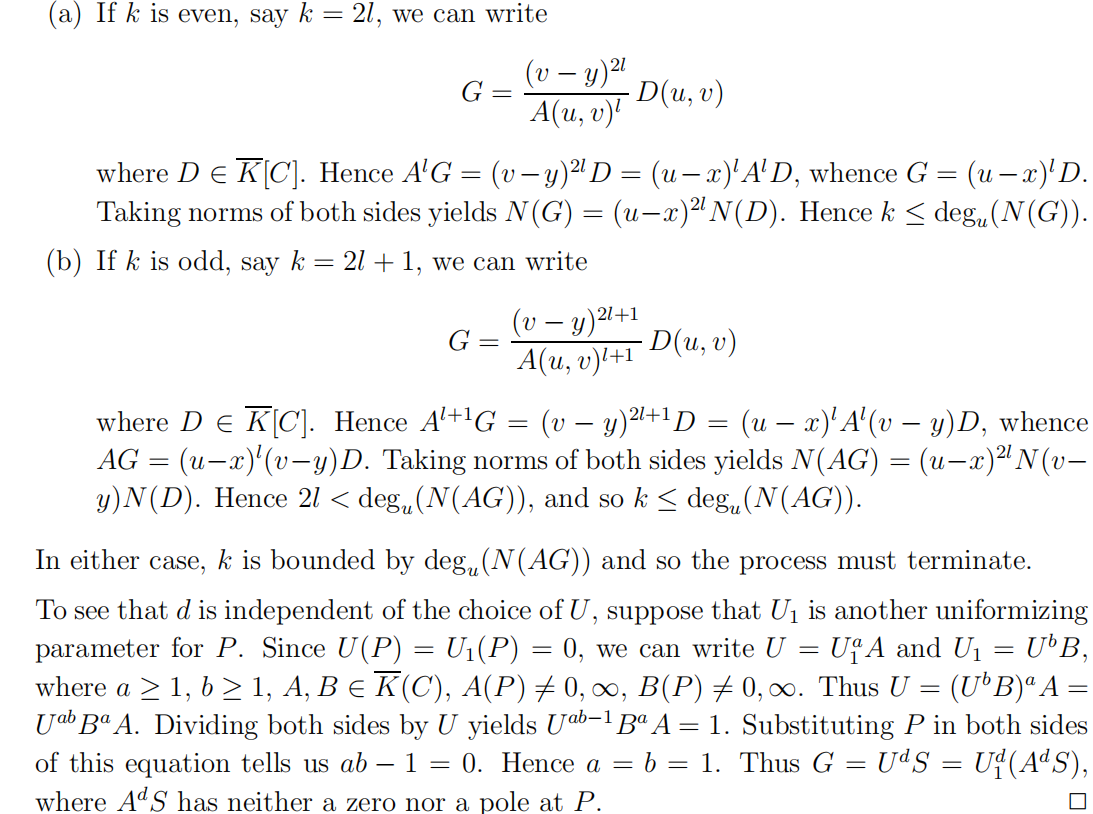
下面利用单值化参数的概念来定义多项式函数在某一点上的阶数。定义26给出了[20]的另一种定义,它更便于用于计算目的。引理27证明这两个定义实际上是等价的。
定义24(多项式函数在一点的阶数的通常定义)令$G\in \bar K[C]^{*} , P\in C , U\in \bar K(C)$是关于$P$的单值化参数,记$G=U^{d}S$,其中$S\in \bar K(C) , S(P)\neq 0,\infty$。$G$的阶在$P$处定义为$ord_{P}(G)=d$。
引理25 令$G_{1} , G_{2}\in \bar K[C]^{*} , P\in C$,记$ord_{P}(G_{1})=r_{1} , ord_{P}(G_{2})=r_{2}$。
$\textrm{(i)}\ ord_{P}(G_{1}G_{2})=ord_{P}(G_{1})+ord_{P}(G_{2})$
$\textrm{(ii)}$若$G_{1}\neq -G_{2}$。若$r_{1}\neq r_{2}$,则$ord_{P}(G_{1}+G_{2})=\textrm{min}(r_{1},r_{2})$,若$r_{1}=r_{2}$则$ord_{P}(G_{1}+G_{2})\geq\textrm{min}(r_{1},r_{2})$
证明:由定义24易证!
定义26(多项式函数在一点的阶数的另一种定义) $G=a-bv\in \bar K[C]^{*} , P\in C$,$G$在$P$处的定义记为$ord_{P}(G)$,定义如下:
$\textrm{(i)}$若$P(x,y)$是有限点,则令$r$为$u-x$能够同时整除$a(u),b(u)$的最高次数,记$G(u,v)=(u-x)^{r}[a_{0}(u)-b_{0}(u)v]$,若$a_{0}(x)-b_{0}(x)y\neq 0$,则令$s=0$;否则,令$s$为$u-x$能整除$N(a_{0}(u)-b_{0}(u)v)=a_{0}^{2}+a_{0}b_{0}h-b_{0}f$。若$P$是一个平凡点,则定义$ord_{P}(G)=r+s$,若$P$是一个特殊点,则定义$ord_{P}(G)=2r+s$。
$\textrm{(ii)}$若$P=\infty$,则$ord_{P}(G)=-max[2deg(a),2g+1+2deg(b)]$。
引理27 定义24与定义26等价。
证明:

引理28 令$G\in \bar K[C]^{*} , P\in C$。则$ord_{P}(G)=ord_{\bar P}(\bar G)$。
证明:

定理29$G\in \bar K[C]^{*}$。则$G$存在有限个零点与极点;此外,$\sum _{P\in C}ord_{P}(G)=0$。
证明:

定义30(有理函数在一点上的阶数)令$R=G/H\in \bar K(C)^{*} , P\in C$,$R$在$P$处的阶数定义为$ord_{P}(R)=ord_{P}(G)-ord_{P}(H)$。
不难证明ordP (R)不依赖于G和H的选择,引理25和定理29对于非零有理函数也成立。
