超椭圆曲线(二)基本定义与属性
定义1(超椭圆曲线)设$K$是一个域,$\bar K$是$K$的代数闭包。$K$上类为$g$的超椭圆曲线定义为如下等式:
其中$h(u)\in K[u]$是次数不超过$g$的多项式,$f(u)\in K[u]$是次数为$2g+1$的首项系数为$1$多项式,并且不存在解$(u,v)\in \bar K\times\bar K$同时满足方程$v^{2}+h(u)v=f(u)\ \textrm{in}\ K[u,v]$与两个偏微分方程$2v+h(u)=0,h^{‘}(u)v-f^{‘}(u)=0$。
所谓$C$上的奇异点是一个解$(u,v)\in \bar K\times\bar K$同时满足上述三个方程。定义$1$表明超椭圆曲线没有任何奇异点。
对于本文的其余部分,假设域$K$和曲线$C$已经固定。
引理1 令$C$是$K$上如式$(1)$定义的超椭圆曲线;
$(\textrm{i})$ 若$h(u)=0$,则$char(K)\neq 2$;
$(\textrm{ii})$ 若$char(K)\neq 2$,则变量替换$u\rightarrow u,v\rightarrow (v-h(u)/2)$将$C$转换为形式$v^{2}=f(u)$,其中$f$的次数为$2g+1$;
$(\textrm{iii})$ 令$C$是形如$(1)$的等式且$h(u)=0,char(K)\neq 2$,则$C$是超椭圆曲线当且仅当$f(u)$在$\bar K$上没有重根;
证明:
$(\textrm{i})$假设$char(K)=2$,则任意的$x\in K , 2x=0$,因此要成为曲线$C$上的奇异点只需要满足如下两个等式即可:
先求满足$f^{‘}(u)=0$的根$u_{0}$,再求满足$v^{2}=f(u_{0})$的根$v_{0}$,从而得到曲线$C$的奇异点$(u_{1},v_{0})$;这与$C$是超椭圆曲线矛盾。
$(\textrm{ii})$经变量替换,$C$的形式为:$(v-\frac {h(u)} {2})^{2}=f(u)\Rightarrow v^{2}=f(u)-\frac {h^{2}(u)} {4}$,而$deg(h)\leq g\Rightarrow deg(f(u)-\frac {h^{2}(u)} {4})=2g+1$。
$(\textrm{iii}) 当h(u)=0,char(K)\neq 2$时,$C$有奇异点等价于存在$(u,v)\in \bar K\times\bar K$,满足:
等价于:
因此,$C$有奇异点等价于存在$u\in \bar K$,满足:
即$f$有重根;因此,$C$是超椭圆曲线等价于$f$无重根。
定义3(有理点,无限点,有限点)设$L$是$K$的扩展域。$C$上$L$有理点的集合,记为$C(L)$,是满足曲线$C$的等式$(1)$的所有点$P(x,y)\in L\times L$连同一个在无穷远处的特殊点(记为$\infty$),点集$C(\bar K)$简单地被$C$定义,$C$上异于$\infty$的点称为有限点。
例4(实数域上的超椭圆曲线)如下是实数域上的超椭圆曲线的三个例子,每条曲线类$g=2$且$h(u)=0$。
$(\textrm{i})\ C_{1}:\ v^{2}=u^{5}+u^{4}+4u^{3}+4u^{2}+3u+3=(u+1)(u^{2}+1)(u^{2}+3)$,$C_{1}$在实平面的图像如图$1$所示;
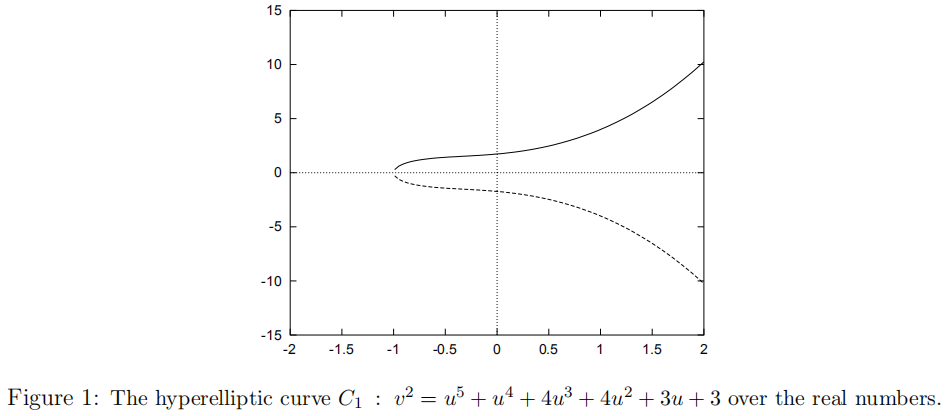
$(\textrm{ii})\ C_{2}:\ v^{2}=u^{5}+u^{4}-u^{2}-u=u(u-1)(u+1)(u^{2}+u+1)$,$C_{2}$在实平面的图像如图$2$所示;
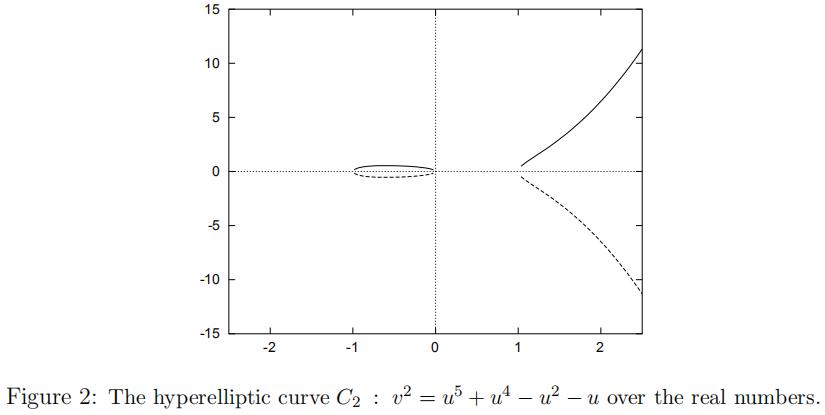
$(\textrm{iii})\ C_{3}:\ v^{2}=u^{5}-5u^{3}-u^{2}+4u=u(u-1)(u+1)(u-2)(u+2)$,$C_{3}$在实平面的图像如图$3$所示;
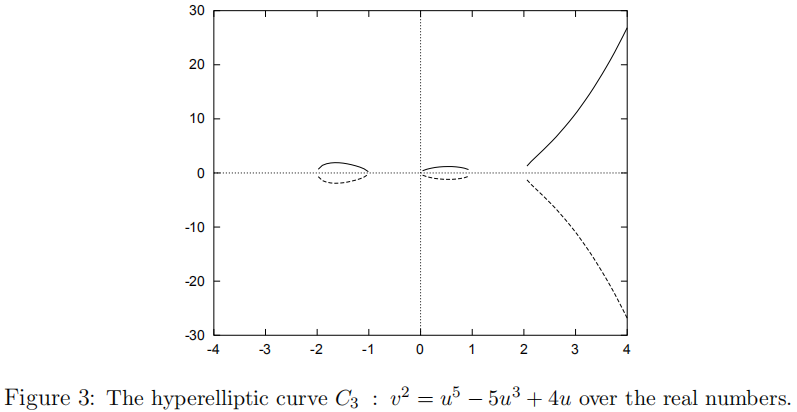
定义5(相反点、特殊点和平凡点)令$P(x,y)$是曲线$C$上的一个有限点。$P$的相反点是$\bar P(x,-y-h(x))$。(注意到$\bar P$确实在$C$上。)我们同样定义$\infty$的相反点$\bar \infty=\infty$为他的本身。若一个有限点$P$满足$P=\bar P$,则该点被称为特殊的;否则,该点被称为平凡的。
例6($Z_{7}$上的超椭圆曲线)考虑有限域$Z_{7}$上的曲线$C:v^{2}+uv=u^{5}+5u^{4}+6u^{2}+u+3$。这里,$h(u)=u,f(u)=u^{5}+5u^{4}+6u^{2}+u+3$且$g=2$,可以证明$C$没有奇异点(除了$\infty$),因此$C$确实是一个超椭圆曲线。$C$上的$Z_{7}$有理点为$C(Z_{7})={\infty,(1,1),(1,5),(2,2),(2,3),(5,3),(5,6),(6,4)}$,点$(6,4)$是一个特殊点。
例7($F_{2^{5}}$上的超椭圆曲线)考虑有限域$F_{2^{5}}=F_{2}[x]/(x^{5}+x^{2}+1)$,并且令$\alpha$是本原多项式$x^{5}+x^{2}+1$在$F_{2^{5}}$的根。$\alpha$的指数如表$1$所示。

考虑有限域$F_{2^{5}}$上类$g=2$曲线$C: v^{2}+(u^{2}+u)v=u^{5}+u^{3}+1$,这里$h(u)=u^{2}+u,f(u)=u^{5}+u^{3}+1$,可以证明$C$没有奇异点(除了$\infty$),因此$C$实际上是一个超椭圆曲线。$C(F_{2^{5}})$中的有限点如下:
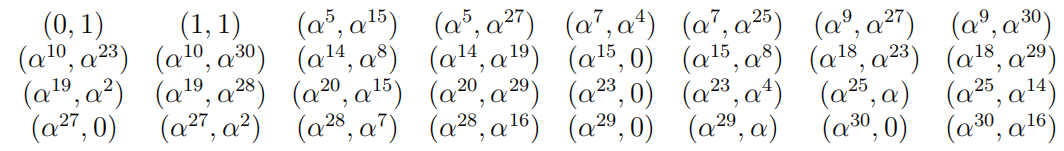
其中,点$(0,1),(1,1)$是特殊的。
