第八章 面向缓存的页置换算法
访问频率置换算法(FBR)
操作系统维护一个如下形式的栈来存放缓存数据:

栈分为3个部分:新区域、中间区域与旧区域;每个缓存块都有一个引用计数,算法具体处理如下:
- 访问的数据在栈中:缓存块被移到栈顶,若缓存块不在新区域,将其引用计数加1;
- 访问的数据不在栈中:在访问完数据之后;栈的旧区域中引用计数最小的缓存块被移出;将访问的数据放到栈顶,其引用计数置1;
FBR算法的问题:需要调整参数。
LRU-K 2Q页置换算法
考虑一下在进程访问数据时,会有哪些模式的访问:
- 顺序访问:数据块一个接一个被访问,不存在重复访问;
- 循环访问:所有的数据块按照一定的间隔重复访问;
- 时间密集访问:最近被访问的数据块是将来最可能被访问的;
- 概率访问:所有数据块都有固定的概率被访问,且被访问的概率相互独立;
LRU-K页置换算法
LRU-K算法是LRU算法的扩展;增加了一个数据访问历史记录队列,记录数据被访问的次数以及最近的访问时间戳。
如果[数据]在离开历史记录队列之前被访问了K次,则需要将[数据]加入数据缓存队列:如果缓存队列的长度超过最大缓存长度,则先将缓存队列头部的数据删除,然后在缓存队列的队尾加上[数据],然后[数据]的访问历史记录从历史记录队列中删除。
若缓存队列的[数据]被访问,则将[数据]放到缓存队列的队尾。
综上,LRU-K页置换算法的示意图如下:
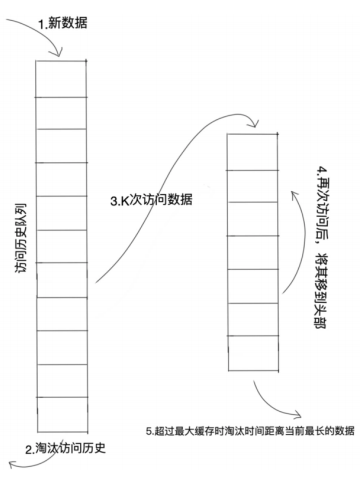
其中,LRU-2是综合考虑各种访问模式后的最优选择。
LRU-2Q页置换算法
进一步改进LRU-2页置换算法;使用两个缓存队列来维护缓存区,示意图如下:
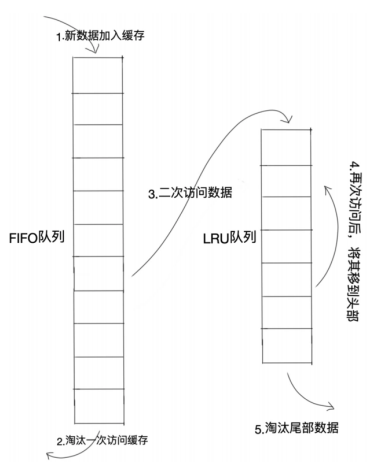
数据块第一次被访问时,数据块缓存到FIFO队列的队尾(如果队列没有空闲空间,就删除队列头部的数据),如果数据块在离开FIFO队列之前被再次访问,则将数据块移到LRU队列的队尾(同样地,如果队列没有空闲空间,就删除队列头部的数据);若LRU队列的数据块被访问,则将数据块放到LRU队列的队尾。
LIRS页置换算法
定义两个属性;R(i,t):从最近一次访问数据块i之后到当前时刻t,被访问的不重复数据块数;IRR(i):在最近两次访问数据块i之间,被访问的不重复数据块数。
初始时,每个数据块的IRR=inf, R=0;
有数据块(记为i)被访问后,每个数据块的IRR值与R值更新:
- 被访问:IRR(i,t)=R(i,t-1), R(i, t)=0;
- 未被访问:IRR(j)不变,R(j,t)=R(j,t-1)+1{最近一次访问数据块j之后到t-1时刻, 数据块i没有被访问过},j!=i;
性质1:每次访问数据块时,除了被访问的数据块,其他数据块的R值均单调不减。
LIRS算法区分IRR值高的数据块与IRR值低的数据块,缓存区分为两个部分:常驻cache与暂驻cache;LIR块(低IRR值的数据块)放在常驻cache,HIR块(高IRR值的数据块)放在暂驻cache;
我们可以看到,R值其实就是IRR值的一个候选,一旦数据块被访问,它的R值就成为IRR值;
由于常驻cache与暂驻cache是根据数据块的IRR值进行区分,那么这两个cache的数据块也会因为其IRR值进行调整;因此,当一个HIR块i被访问后,若存在LIR块j,R(j,t)>size且R(j,t)>IIR(i),则数据块i与数据块j的状态交换。即max{R(j,t)|j in LIR}>max{size, IIR(i)}。
LIRS算法在各种访问模式下均有很好的表现,但是算法要维护两组值(R值与IRR值)使得算法的开销很大;因此,也就有了下面利用栈而不用显式计算R值与IRR值的方法。
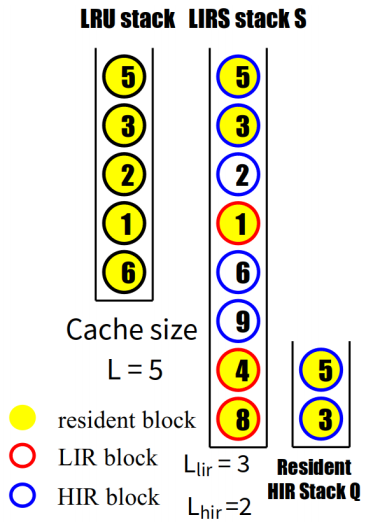
维护两个栈:栈S与栈Q;
栈S:LIR块(低IRR值的数据块)与IRR值小于LIR块的最大R值的HIR块(高IRR值的数据块);
栈Q:常驻cache中的HIR块;
事实上,栈S存放着当前的LIR块与之后有可能成为LIR块的HIR块;下面介绍”栈裁剪”操作。
“栈裁剪”操作:若栈S底部的LIR块被删除,则一直删除底部数据块直到遇到LIR块。
Q:”栈裁剪”操作的合理性是什么?
A:若栈S底部的LIR块被删除,则底部的HIR块将不会成为LIR块。
在证明”栈裁剪”操作的合理性之前,注意到如下的性质:
性质2:记S栈如下:
1 | --------------------------------------- |
那么R(q_i, t)>R(q_i+1, t),即R(q_i, t)>=R(q_i+1, t)+1。
对栈底部的HIR块i,考虑它再次被访问后:IRR(i)=R(i,t-1)>max{R(j,t-1)|j in LIR} => IRR(i)>=max{R(j,t)|j in LIR};从而状态交换的条件不成立,因此栈底部的HIR块不会成为LIR块;
考虑访问各种数据块时算法的反应:
1 | | |
