文章目录

本节考察字符串查找问题：在主串T中寻找模式串P。普遍的情况是，T的某部分与P的一部分匹配，但是并没有完全匹配；这时平凡的想法是模式串移一位，然后重新检查，但是这样复杂度非常高；

KMP算法希望利用这部分匹配的信息，保证不重复考察主串中的元素。

 

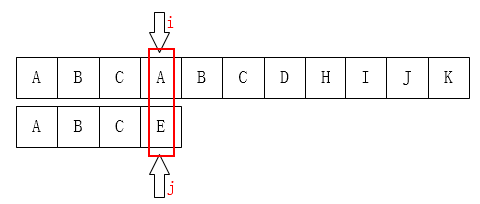
第一次匹配失败后并没有模式串移动一位然后重新检查，而是直接将模式串移到如下位置。

 

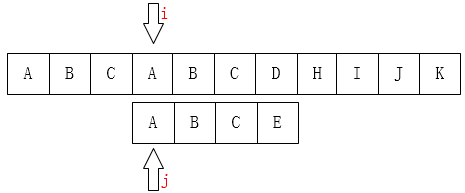
这就是KMP算法的高明之处，主串中的i指针不变，模式串中的j指针回退。因此，下面的关键就是j应该回退到何处。

由于j可能在模式串中任一位置回退，因此将所有j要回退的位置存到数组next中。

KMP算法与平凡想法重合的一种情况是j=0回退时，都是将模式串右移一位重新检查，因此next[0]=-1；

求解next数组的方法类似”数学归纳法”，假设已知所有不大于j的r的next值，且记next[j]=k，下面介绍如何求得next[j+1]。

如上图，j回退到k则须P[0 : k-1]=T[i-k : i-1]，再根据部分匹配的信息：T[i-k : i-1]=P[j-k : j-1]从而P[0 : k-1]=P[j-k : j-1]，这就是k作为next[j]的定义；

那么next[j+1]应满足：P[0 : next[j+1]-1]=P[j+1-next[j+1] : j]；从而那些P[0 : m]=P[j-m-1 : j-1]的m可作为next[j+1]-2的候选值，在P[m+1]=P[j]时m+2便是next[j+1]！

如何得到所有的m？

由next[j]定义可知它必然小于j，故next[k]也是已知的：P[0 : next[k]-1]=P[k-next[k] : k-1]联立P[0 : k-1]=P[j-k : j-1]可得P[0 : next(k)-1]=P[j-next[k] : j-1]，可见next[k]-1就是m的一个候选值；

以此类推，next[next[k]]-1…都是m的一个候选值，当其中的某个m满足P[m+1]=P[j]时就得到next[j+1]=m+2；即next[j+1]是k+1、next[k]+1、next[next[k]]+1、…中的一个。

例外：所有的m均不满足P[m+1]=P[j]，则next[j+1]=-1。

最后给出求解next数组的伪代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
def getNext(s):
    m=len(s)
    Next=[0]*m
    Next[0]=-1
    jth, k=1, -1
    while jth<m:
        while k>=0 and s[jth]!=s[k+1]:
            k=Next[k]
        if s[jth]==s[k+1]:
            k+=1
        Next[jth]=k
        jth+=1
    return Next