第七章第三节 网络流问题
给定边容量为c(v, w)的有向图G=(V, E),其中有一个起点,记为s,有一个收点记为t,最大流问题就是求出从s到t可以通过的最大流量。
为求取最大流,首先使用贪婪算法求出一个流量相对较大的流,然而这样求出的流所通过的流量并不一定是最大的,还需要进行一系列的修正过程。
简单的最大流算法
该算法能求出相对较大流量的流,后续还需要修正过程。
初始:图对应的流图各边的流量均为0,残余图与图相同,如下图所示。
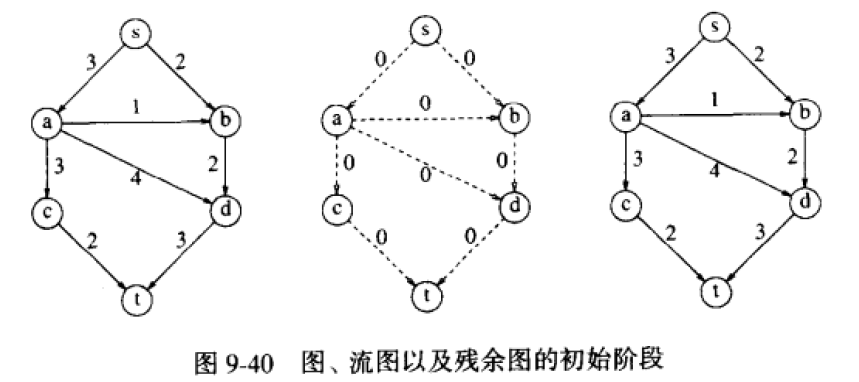
循环:
- 寻找残余图中从s到t的一条路径,这条路径可以通过的流量为该路径上每条边流量的最小值,记为D;
- 在流图中该路径上每条边的流量增加D;
- 在残余图中该路径上每条边的流量减少D,若残余图中有的边流量为0,则将其从残余图中删除。
退出:残余图中不存在从s到t的路径。
退出时,流图中的流就是找到的一个流量较大的流。但是这个流不一定是最大流,还需要如下的修正过程。
修正
给定图G及其上的流f,它对应的增广图G_f定义如下:对图G中任一条边(u, v)
- (u, v)在流中且f(u, v)小于c(u, v),则增广图中有一条从u到v的边,其流量为c(u, v)-f(u, v);还要一条从v到u的边,其流量为f(u, v);
- (u, v)在流中且f(u, v)=c(u, v),则增广图中有一条从v到u的边,其流量为f(u, v);
- (u, v)不在流中,则增广图中有一条从u到v的边,其流量为c(u, v);
于是,修正过程如下。
循环:给定图G及其上的流f,它对应的增广图G_f,在增广图中寻找一条从s到t的路径,根据找到的路径修改流f。
具体修正过程为:对路径中的边(u, v)
- 若(u, v)已在f中,则f(u, v)加上路径上的流量即可;
- 若(v, u)在f中,则f(u, v)减去路径上的流量;
- 若(u,v)不在f中,则将(u,v)加到流中,f(u, v)为路径上的流量;
退出:增广图中不存在一条从s到t的路径,退出循环;此时的流f就是最大流。
参考链接
