文章目录
  1. 散列函数
  2. 分离链接法
  3. 开放定址法
    1. 线性探测法
    2. 平方探测法
    3. 双散列
  4. 再散列
  5. 可扩散列

散列函数

散列表通过散列函数将每个关键字映射到0至Tabsize-1中的某个数X，然后将该关键字放在散列表第X项；下面的问题就是如何选择一个好的散列函数。

不管如何选择散列函数，总会产生冲突，因为关键字的个数比散列表的长度要大。解决冲突的方法有：分离链接法与开放定址法。

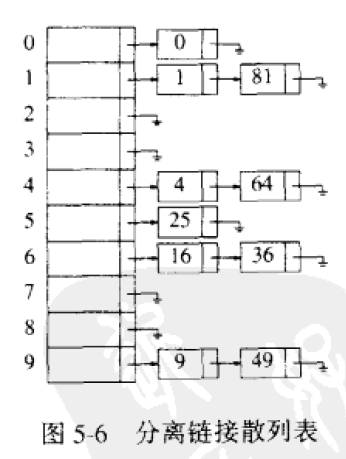
分离链接法

将映射到同一项的关键字用链表组织起来，如下图所示。

 

开放定址法

在冲突发生时，尝试将关键字放到另外的项。下面介绍三个具体的算法。

线性探测法

冲突函数是线性函数，即以固定步长考察散列表(可绕回)，直到找到空单元。

平方探测法

冲突函数是平方函数，用来解决聚集问题；即步长依次为1、4、9等等(这里二次项系数为1)。

双散列

如冲突函数$F(i)=i\cdot hash_{2}(X)$，$hash_{2}$是另外一个散列函数。

再散列

对于使用平方探测的开放定址散列表，若表的元素填到一定程度，插入将会消耗时间过长甚至可能失败。解决的办法是建立一个大约原长度两倍的散列表，并将原散列表中的元素重新计算后填入新散列表。上述过程就是再散列。

再散列的时刻可以有多种选择方案：(1)表满一半即再散列；(2)当插入失败时即再散列；(3)途中策略：当散列表的装填因子(散列表的元素个数/散列表大小)到达某个值时。

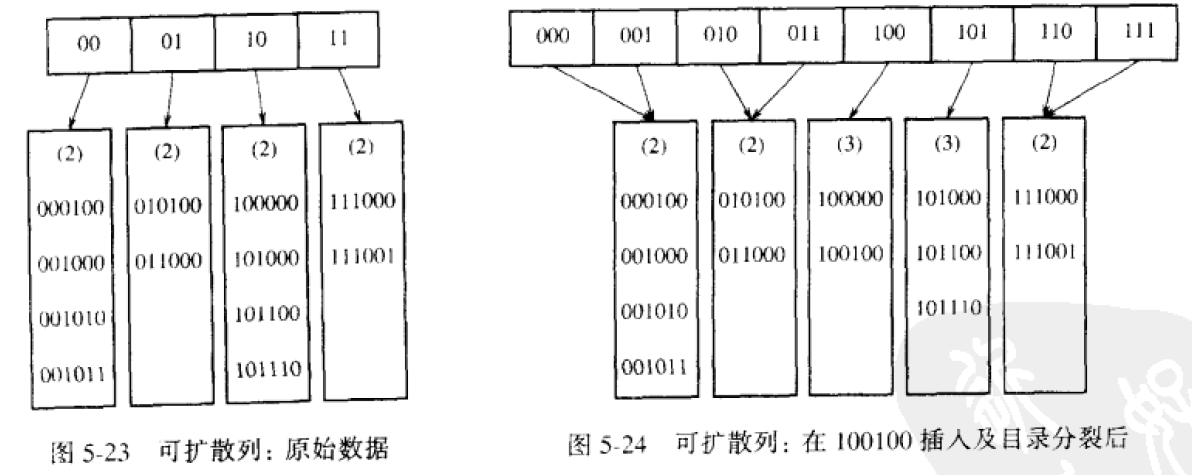
可扩散列

取关键字若干比特，作为”目录”，每个树叶的这些比特相同，每个树叶最多可容纳M个关键字，若一个树叶关键字个数超过M则”目录”再加一个比特，如下图所示。