第二章第七节 红黑树
红黑树的定义
AVL树的一个流行的变种就是红黑树。红黑树是具有下列着色性质的二叉查找树。
- 每一节点或着成红色,或着成黑色;
- 根节点为黑色;
- 红色节点的子节点必须是黑色;
- 任一节点到NULL指针的每一条路径必须包含相同数目的黑色节点;
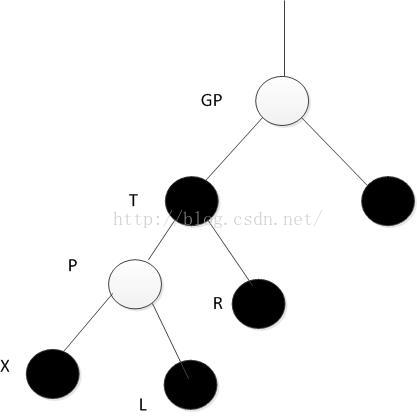
如下图是一个红黑树的示例。
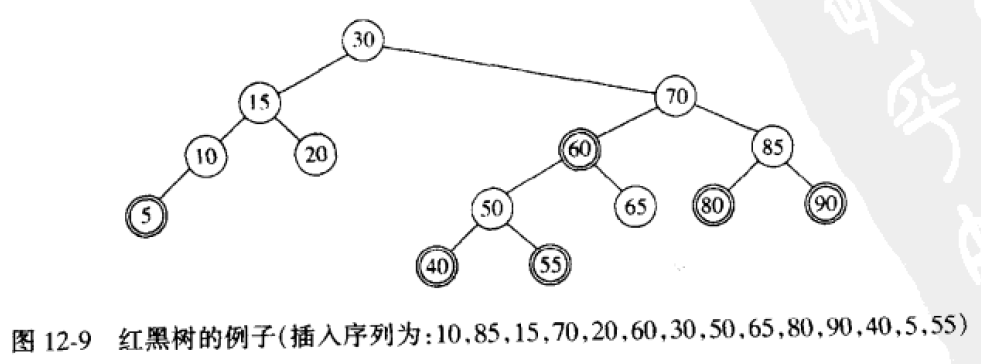
注:红黑树是AVL树的变种,不再严格遵守AVL树的要求;对红黑树的插入即对二叉查找树的插入再加上一定的调整。
插入-自底向上调整
承认一个事实:根据第四条性质,插入的节点必须涂成红色!此时,若父节点就是黑色,则插入完成;否则与第三条性质冲突,必须对该树进行调整,调整包括改色与旋转。
注意到红黑树也是AVL树,在插入的时候也需要进行对应的旋转操作;当插入完成后,还需要进行调整以满足红黑树的性质。记插入的节点为X,(已插入的)X的父节点为P,P的兄弟节点为S。
若S是黑色节点,此时X与S的”搭配”有两种情形(每种都有对称情形)。所做的调整如下。
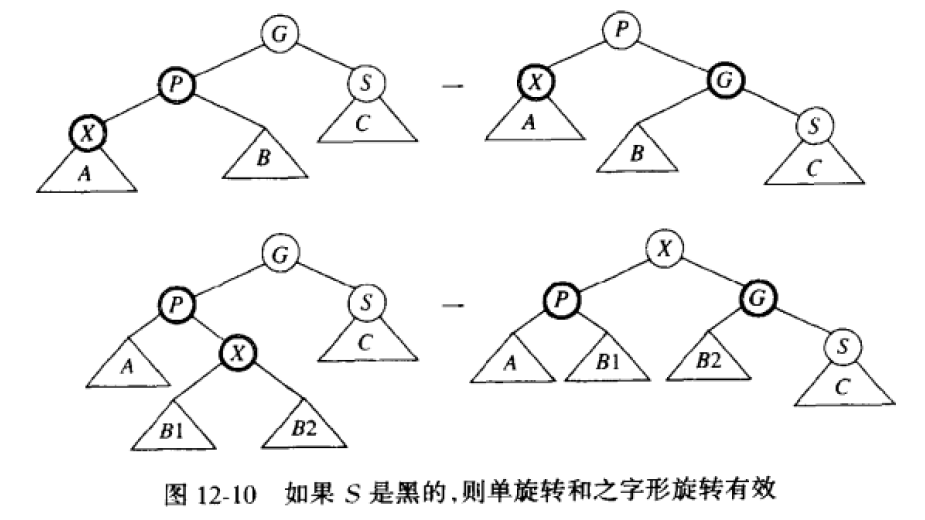
调整之后红黑树的性质满足。
若S为红色节点,再做如上图的调整仍不满足红黑树的性质,只能继续调整。
由于S此时为红色节点,使得新树不满足第三条性质,故需要进行调整;同时,为了保证第四条性质,P-G-S中只能有一个黑色节点,因此只能将P、S涂成红色,G涂成黑色。若P的父节点为黑色节点,则插入完成;
否则,还需要进行调整,记P的父节点为Y,则此时的(P , Y)就是初始时的(X, P),因此对其进行同样的处理,直到某个”父节点”的兄弟节点为黑色节点或到达根节点(根节点为黑色节点,因此递归一定能结束)。
插入-自顶向下调整
插入之后自底向上调整需要一个栈来保存查找路径上的节点;事实上,插入也可以采用自顶向下的方式,在查找的过程中对树进行调整以保证”S”始终为黑色节点!
对遍历的节点X,若X的两个子节点均为红色,由第三条性质,X必为黑色节点,将X与其子节点进行颜色对换,若X的父节点为黑色,则在X处的调整完成;
否则,注意到X的父节点为红色,因此X的父节点的兄弟节点一定不是红色(否则会与它们的父节点进行颜色对换,从而X的父节点不会为红色),因此可使用上图中的旋转进行处理。
查找完成之后,将待插入节点插入路径终点对应子节点。
注:在具体实现中,使用两个标记节点:根与NullNode;根标记将存储关键字$\infty$以及指向真正根的右指针;
自顶向下删除
对于要删除的节点,有以下几种可能:叶节点、双子节点,单支红子黑节点;因为以下四种单支情况不可能出现。
对于删除的任意非叶节点X,若它有右子树,则用右子树上的最小值节点将其替换(颜色使用X的颜色),若X无右子树,那么它一定有左子树,则用左子树上的最大值节点将其替换(颜色使用X的颜色),那么删除的节点就变为右子树上的最小值节点;
这个节点最多有一个右子节点(左子节点),如果它有一个右子节点(左子节点),那么将它删除之后使用子节点涂黑补位即可!
否则,删除的就是叶节点,若这个叶节点为红色,直接删除即可!
否则,就是要删除一个黑色叶节点。
综上,所有的情况都能转换成删除一个叶节点,若叶节点为红色,直接删除即可!否则,就是删除一个黑色叶节点。删除黑色叶节点可采用自底向上或自顶向下的方式,自底向上的方式过于复杂,感兴趣可参考July对红黑树的讲解;相比之下,自顶向下的删除有一个自始至终的目标——保证当前节点为红色。
1 | 初始:将根节点涂红; 当前节点记为X, X的兄弟节点记为T, X的父节点记为P |
X的子节点均为黑色
(1) T的子节点亦全为黑色;则P、T、X颜色翻转即可;
(2) T有一个红子节点,根据这个红子节点是左或右,进行如下图的旋转;
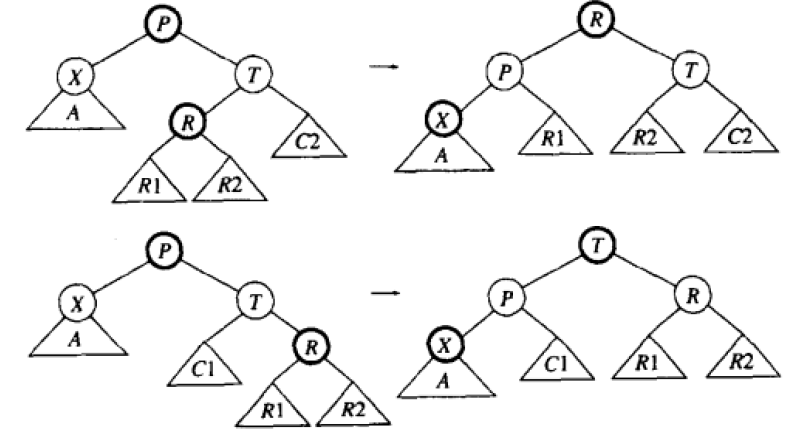
X有红节点
先下降,若X落到红子节点,则继续下降即可;否则,将P、T进行颜色翻转,然后旋转P与T重新进入P红X黑T黑的情形。
参考链接
