文章目录
  1. 自顶向下伸展
  2. 插入
  3. 删除

自顶向下伸展

由于常规的伸展树需要从根节点遍历至对应叶节点再返回，这需要大量的内存开销，且必须处理很多特殊情况；因此，本节介绍自顶向下伸展树。

在查找的同时，进行”自顶向下”展开，下面介绍针对三种情况下(对称情况略)的展开操作。

单旋转

 

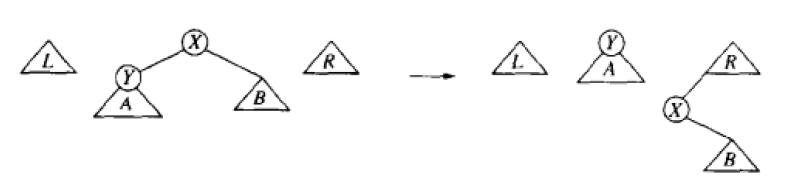
一字型

 

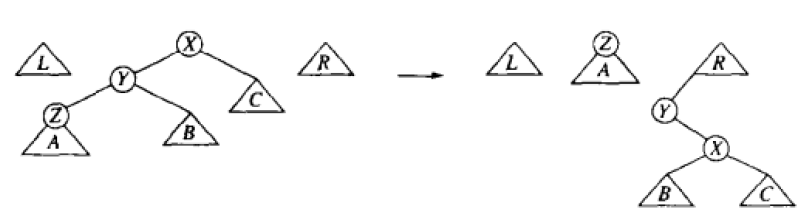
之字型

 

其中，树L、R初始时为空，在展开的过程中不断添加节点；于是，在查找到达所在节点时，原来的一个树变成三个树，合并方法如下。

 

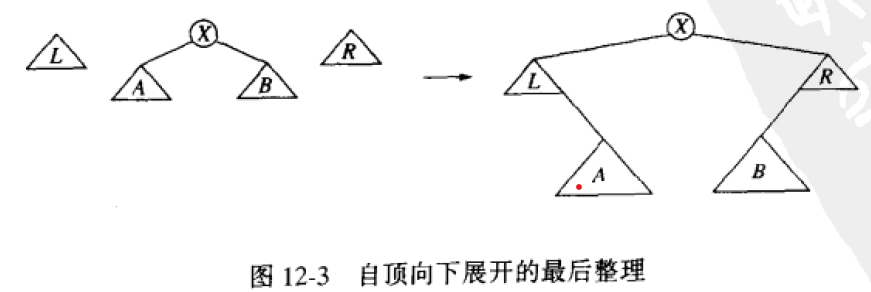
此外，之字型的旋转还有简化版。

 

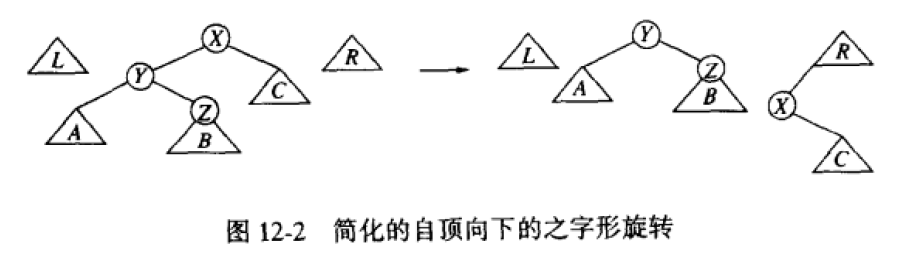
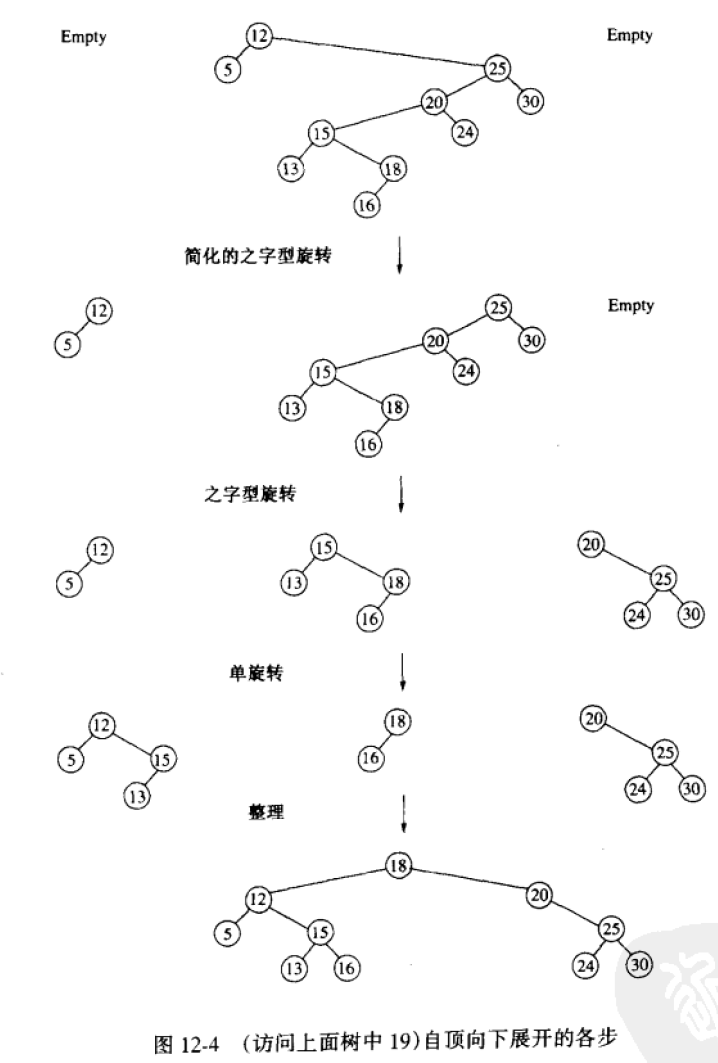
最后，给出一个自顶向下树的例子(其中”之字型旋转”注释有误，应为”一字型旋转”)。

插入

为待插入节点分配一个新的指针。若树为空，则直接建立一棵单点树。否则，将树自顶向下伸展为一棵新树，新树的根节点记为NR。

  • 若待插入节点X的键值key(X)=key(NR)，则新树有X的一个复制拷贝；
  • 若待插入节点X的键值key(X)>key(NR)，则NR及其左子树成为X的左子树，NR的右子树成为X的右子树；
  • 若待插入节点X的键值key(X)<key(NR)，则NR及其右子树成为X的右子树，NR的左子树成为X的左子树；

删除

首先，在查找待删除节点X的同时将树自顶向下伸展为一棵新树NT，若NT的根节点为X(考虑到X在原树中可能不存在，因此需要判断)

  • 若NT的左子树为空，则将NT的右子树作为返回值即删除了待插入节点；
  • 否则，在NT的左子树NL中查找X的同时将NL自顶向下伸展为一棵新树NNL，由于NL中节点的键值均小于X的键值，因此NNL的根节点没有右子树，于是将NT的右子树接到NNL的根节点上(作为其右子树)即可；