第二章第五节 B-树
B-树的定义
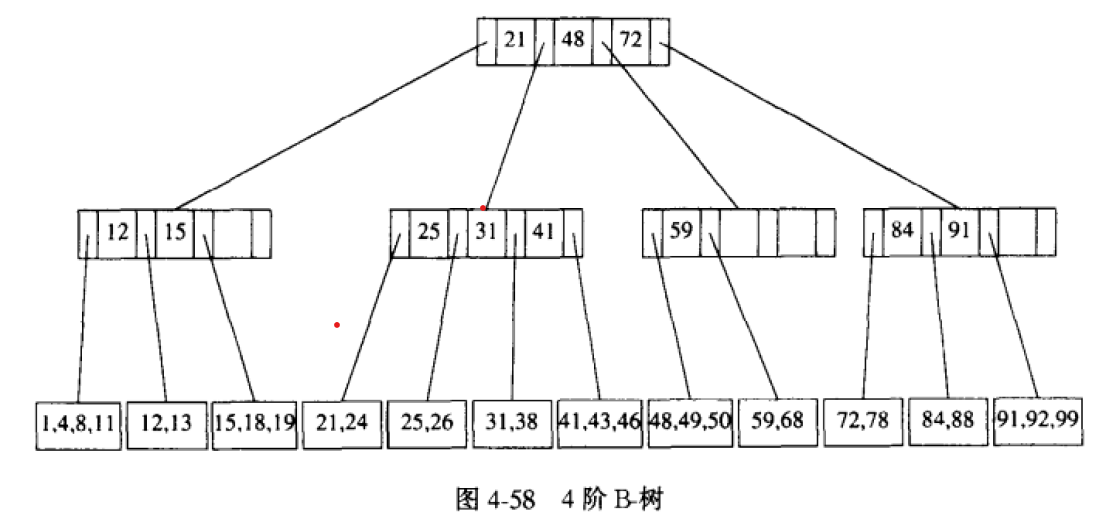
阶为M的B-树是具有下列结构特性的树。
- 树的根或是一片树叶,或者子节点数在2-M之间;
- 除根节点外,所有非叶节点的子节点数在$\lceil (M+1)/2\rceil$-M之间;
- 叶节点中关键字的个数在$\lceil (M+1)/2\rceil$-M间,且所有树叶均处于同一深度;
使用B-树组织数据时,数据都存储于叶节点。而非叶节点存储指向各子节点的指针$P_{0},…,P_{M-1}$以及在以这些子节点(除第一个)为根节点的子树上的最小值$k_{1},…,k_{M-1}$,其中有些指针可能为NULL,则对应的$k_{i}$也是未定义的。并且,各兄弟节点之间具有如下性质。
因此,在每个非叶节点处经O(logM)次判断可找到接下来要查找的分支。下面介绍在B-树上的查找、插入与删除操作。
查找
记B-树的根为R,要查找的值为y;在每个非叶节点,记它的各子节点的指针$P_{0},…,P_{M-1}$以及在以这些子节点(除第一个)为根节点的子树上的最小值$k_{1},…,k_{M-1}$,则需要找到满足条件$k_{i}\leq y<k_{i+1}$的$i$,使用二分查找可在O(logM)的时间内找出。最后到达叶节点,在叶节点上进行二分查找即可。
插入
开始的操作与查找相同,在找到对应的叶节点N后,将其插入到叶节点N中。
插入之后,要考虑叶节点N是否可以容纳,若不能容纳,则叶节点N需要”分裂”,两个叶节点分别拿走原叶节点的$\lceil (M+1)/2\rceil$、$\lfloor (M+1)/2\rfloor$个节点;
由于这时叶节点N的父节点多了一个子节点,因此,需要考虑N是否可以容纳,同样地,若不能容纳,则N的父节点也需要”分裂”;
以此类推,沿着查找路径返回至根节点的同时将不能容纳子节点的节点”分裂”,以及各非叶节点的更新。
删除
到达对应叶节点N后,删除相应关键字,若叶节点N的关键字个数仍在$\lceil (M+1)/2\rceil$-M之间,再沿着查找路径返回至根节点的同时更新非叶节点。
否则,考虑(左右)兄弟节点能否在满足关键字数在$\lceil (M+1)/2\rceil$-M之间的条件下,”分”一些关键字至N使得N的关键字数在$\lceil (M+1)/2\rceil$-M之间;若能,则左右兄弟节点”分”一些关键字至N,同时更新这三个叶节点。
否则,需要删除叶节点N,然后将叶节点N的关键字”分”到左右兄弟节点中,然后将左右兄弟节点更新;此时,N的父节点也少了一个子节点,同样可能出现子节点数不够的情况,处理方式与上述类似;以此类推,沿着查找路径返回至根节点的同时进行相应操作。
B+树
B+树在B-树的基础上,增加了叶节点之间的双向链表。由于增加了双向链表,在插入与删除时也需要维护双向链表。
