文章目录
  1. 二叉查找树的定义
  2. 查找
  3. 最值
  4. 插入
  5. 删除

二叉查找树的定义

二叉树的一个重要应用——二叉查找。二叉树是二叉查找树当且仅当对于树中的每个节点X，它的左子树上所有节点的值小于X的值，它的右子树上所有节点的值大于X的值。

关于二叉查找树，有置空、查找、最大值、最小值、插入、删除操作。

查找

记二叉查找树的根为R，要查找的值为y；则判断key(R)是否等于y，若相等，则查找完毕；否则，若key(R)>y，则在R的左子树上查找；若key(R)<y，则在R的右子树上查找。以此类推，直到查找到键值为y的节点或未能找到。

最值

最小值：从二叉查找树的根节点开始，一直向左直到节点无左子节点；最大值同理，从二叉查找树的根节点开始，一直向右直到节点无右子节点。

插入

对于一个二叉查找树，现插入键值为y的节点；寻找待插入节点的位置要遍历路径与查找操作的遍历路径一样，不同的是，在遍历的最后，将待插入节点放在下一步将遍历的位置。

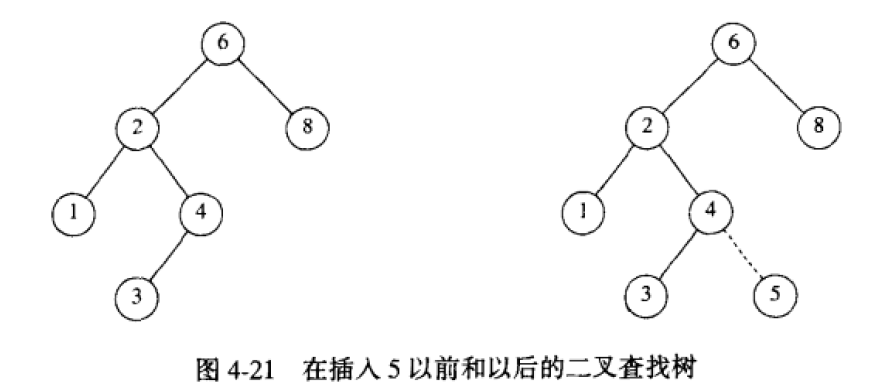
如下图所示，待插入节点的键值为5，它遍历的路径为6=>2=>4，下一步将要遍历键值为4的节点的右子树，可键值为4的节点无右子树，因此键值为4的节点就是遍历的终点，而待插入节点下一步将遍历的是其右子节点，故将待插入节点放在其右子节点。

删除

删除的情形比较复杂，下面分类讨论。

  • 被删除的节点是叶节点，则直接删除或打上删除标记即可；
  • 被删除的节点有一个子节点，则被删除的节点之父节点调整指向被删除的节点的指针为指向被删除的节点的子节点；
  • 被删除的节点有两个子节点，则使用其右子树的最小键值节点替换，然后删除在原位置的最小键值节点，由于在原位置的最小键值节点一定没有左子树(参见最值)因此删除原位置的最小键值节点转换为上一情形；